본 게시글은 2024년 상/하반기 코딩테스트를 보다 체계적으로 준비하기 위해, 코딩 테스트 알고리즘을 정리한 글이다.

실전 코딩 테스트를 진행하면서도 이 페이지의 게시글을 참고하면 해당 문제를 해결하기 위해 어떤 알고리즘을 써야 하는지 결정 할 수 있는 가이드라인이 될 것으로 기대한다.

📘 코딩 테스트 준비 오버뷰

코딩테스트에 필요한 2가지 기본 소양

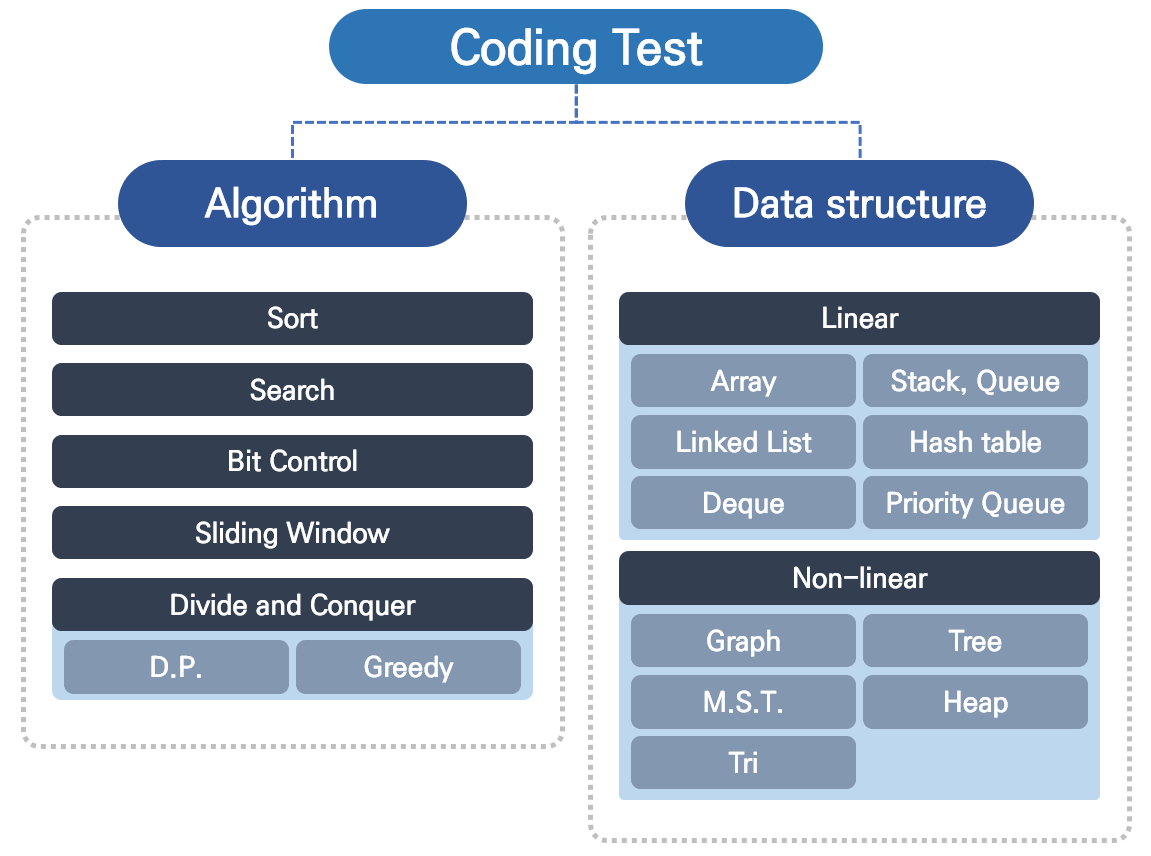
코딩 테스트는 위와 같이 크게 자료구조와 알고리즘쪽으로 구분 할 수 있을 것이다.

이번 포스트에서는 이 2가지 내용을 잘 정리해서 언제든 쉽게 찾아볼 수 있도록 한다.

다만, 알고리즘쪽 관련 포스트는 코딩테스트 이론 공부 2편을 참고하면 된다.

자세한 설명은 생략한 부분도 많다! (내가 볼 용으로 만들었기 때문)


본 내용은 cpp을 기준으로 작성되었다.

🗄️ 자료 구조

🔶 I. 선형 구조

💠 Array

배열은 연속된 변수들을 저장하고 관리 할 수 있는 가장 간단한 자료구조이다.

검색은 매우 빠르나 추가/제거가 불편하다는 단점이있다.

int testArray[] = {1,2,3,4};

💠 List(Vector)

배열과 다르게 길이나 용량을 가변적으로 정할 수 있다는 장점이 있다.

배열보다는 조금 느리다는 단점이 있다.

#include <vector>

vector<int> testVector_1;             // 빈 벡터 만들기
vector<int> testVector_2(5);            // 원소 5개로 만들기
vector<int> testVector_3(testVector_2); // 다른 벡터로 만들기

🔶 II. 비선형 구조

💠 Map

인덱스로 int가 아닌 다른 자료형을 사용할 수 있는 트리

cpp의 map은 검색,삽입,삭제가 n log(n)인 red black tree로 구현되었다.

#include <map>

map<char,int> m;
map<char,int>::iterator it;

m['B'] = 2;                        //m : (B,2)
m.insert(make_pair('A',1));        //m : (A,1) (B,2)
m['C'] = 3;                        //m : (A,1) (B,2) (C,3)

m.erase('A');                      //m : (B,2) (C,3)

//m전체를 순회하며 key와 value 출력
for(it = m.begin(); it != m.end(); it++)
    cout << it->first << ' ' << it->second << '\n';

if(m.find('B') != m.end())
    cout << "노드가 존재합니다." << '\n';
else
    cout << "노드가 존재하지 않습니다." << '\n';

중복을 허용하지않기 때문에, 중복되는 key값을 입력받으면 무시한다.

코드 출저 : 공대사람의 ‘주니어 개발자의 대나무숲’ 블로그

💠 Set

key만 있는 map 혹은 정렬된 집합

특징은 set은 key와 value가 같다는 것이다.

#include <set>

set<int> s;
set<int>::iterator it;

s.insert(4);               //s : 4
s.insert(1):               //s : 1 4
s.insert(2);               //s : 1 2 4

vector<int> v;
v.push_back(3);            //v : 3
v.push_back(5);            //v : 3 5
v.push_back(6);            //v : 3 5 6

s.insert(v.begin(), v.end());        //s : 1 2 3 4 5 6

s.erase(4);                //s : 1 2 3 5 6
s.erase(s.begin());        //s : 2 3 5 6

//지울 원소를 입력받음
int toErase;
scanf("%d", &toErase);

it = s.find(toErase);

//지울 원소가 존재하는 원소일 때만 지움
if(it != s.end())
    s.erase(it);

코드 출저 : 공대사람의 ‘주니어 개발자의 대나무숲’ 블로그







🍷 자주사용하는 코드 스니펫

🔶 I. 수학 관련 관련

💠 에라토스테네스의 체 : 소수 찾기

1부터 n까지의 자연수 중에서 모든 소수를 찾아내는 코드이다.


#include <iostream>
#include <cmath>
using namespace std;

int number = 120; // 구하고자 하는 소수의 범위
bool primeNum[121];

void primeNumberSieve()
{
    // primeNum 배열 초기화
    for (int i = 2; i <= number; i++)
    {
        primeNum[i] = true;
    }

    for (int i = 2; i <= sqrt(number); i++)
    {
        // primeNum[i] 가 false이면 이미 소수가 아니므로 continue
        if (primeNum[i] == false)
            continue;
        // i*k (k<i) 까지의 수는 이미 검사했으므로 j는 i*i 부터 검사해준다.
        for (int j = i * i; j <= number; j += i)
            primeNum[j] = false;
    }
}

코드 출저 : [Algorithm] 에라토스테네스의 체 - C++


💠 소인수 분해

1부터 n까지의 자연수 중에서 모든 소수를 찾아내는 코드이다.


int n = 120;
vector<int> vec;
for(int i=2; i*i<=n; i++) {
    while( n % i==0 ) {
        vec.push_back(n);
        n/=i;
    }
}

if( n > 1 ) 
    list.push_back(n);

코드 출저 : [알고리즘] 소수(Prime Number) 구하기 - 에라토스테네스의 체 (Java)


💠 최대 공약수 구하기


int gcd(int a, int b)
{
    int temp;
    while ( b != 0 ) {
        temp = a % b;
        a = b;
        b = temp;
    }
    return a;
}

코드 출저 : [c++] c++ 최대 공약수


💠 최대 공약수 구하기

두 수 a, b의 최대 공약수를 gcd(a,b), 최소 공배수를 lcm(a,b)라고 할 때, 다음이 성립함

a * b == gcd(a,b) * lcm(a,b)

따라서, 최대 공약수는 아래와 같음

int lcm(int a, b)
{
    return a * b / gcd(a, b);
}

코드 출저 : C++ - 최대공약수와 최소공배수 구하기


💠 에라토스테네스의 체 : 소수 찾기

1부터 n까지의 자연수 중에서 모든 소수를 찾아내는 코드이다.


코드 출저 : [Algorithm] 에라토스테네스의 체 - C++


🔶 II. 문자열 관련

💠 cpp 문자열 split

#include <sstream>

vector<string> split(string input, char delimiter) {
    vector<string> answer;
    stringstream ss(input);
    string temp;
 
    while (getline(ss, temp, delimiter)) {
        answer.push_back(temp);
    }
 
    return answer;
}